Theory of ANN
An artificial neural network is a supervised learning algorithm which means that we provide it the input data containing the independent variables and the output data that contains the dependent variable. For instance, in our example our independent variables are X1, X2 and X3. The dependent variable is Y.
In the beginning, the ANN makes some random predictions, these predictions are compared with the correct output and the error(the difference between the predicted values and the actual values) is calculated. The function that finds the difference between the actual value and the propagated values is called the cost function. The cost here refers to the error. Our objective is to minimize the cost function. Training a neural network basically refers to minimizing the cost function. We will see how we can perform this task.
A neural network executes in two phases: Feed Forward phase and Back Propagation phase. Let us discuss both these steps in detail.
Feed Forward

In the feed-forward phase of ANN, predictions are made based on the values in the input nodes and the weights. If you look at the neural network in the above figure, you will see that we have three features in the dataset: X1, X2, and X3, therefore we have three nodes in the first layer, also known as the input layer.
The weights of a neural network are basically the strings that we have to adjust in order to be able to correctly predict our output. For now, just remember that for each input feature, we have one weight.
The following are the steps that execute during the feedforward phase of ANN:
Step 1: Calculate the dot product between inputs and weights
The nodes in the input layer are connected with the output layer via three weight parameters. In the output layer, the values in the input nodes are multiplied with their corresponding weights and are added together. Finally, the bias term b is added to the sum.
Why do we even need a bias term?
Suppose if we have a person who has input values (0,0,0), the sum of the products of input nodes and weights will be zero. In that case, the output will always be zero no matter how much we train the algorithms. Therefore, in order to be able to make predictions, even if we do not have any non-zero information about the person, we need a bias term. The bias term is necessary to make a robust neural network.
Mathematically, the summation of dot product:
X.W=x1.w1 + x2.w2 + x3.w3 + b
Step 2: Pass the summation of dot products (X.W) through an activation function
The dot product XW can produce any set of values. However, in our output, we have the values in the form of 1 and 0. We want our output to be in the same format. To do so we need an Activation Function, which restricts the input values between 0 and 1. So of course we’ll go ahead with Sigmoid activation function.


The sigmoid function returns 0.5 when the input is 0. It returns a value close to 1 if the input is a large positive number. In the case of negative input, the sigmoid function outputs a value close to zero.
Therefore, it is especially used for models where we have to predict the probability as an output. Since the probability of anything exists only between the range of 0 and 1, sigmoid is the right choice for our problem.
In the above figure z is the summation of dot product X.W
Mathematically, the sigmoid activation function is:
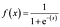

Let us summarize what we have done so far. First, we have to find the dot product of the input features(matrix of independent variables) with the weights. Next, pass the summation of dot products through an activation function. The result of the activation function is basically the predicted output for the input features.
Back Propagation
In the beginning, before you do any training, the neural network makes random predictions which are of course incorrect.
We start by letting the network make random output predictions. We then compare the predicted output of the neural network with the actual output. Next, we update the weights and the bias in such a manner that our predicted output comes closer to the actual output. In this phase, we train our algorithm. Let’s take a look at the steps involved in the backpropagation phase.
Step 1: Calculate the cost
The first step in this phase is to find the cost of the predictions. The cost of the prediction can be calculated by finding the difference between the predicted output values and the actual output values. If the difference is large then cost will also be large.
We will use the mean squared error or MSE cost function. A cost function is a function that finds the cost of the given output predictions.
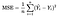

Here, Yi is the actual output value and Ŷi is the predicted output value and n is the number of Observations.
Step 2: Minimize the cost
Our ultimate goal is to fine-tune the weights of our neural network in such a way that the cost is minimized the minimum. If you notice carefully, you’ll get to know that we can only control the weights and the bias. Everything else is beyond our control. We cannot control the inputs, we cannot control the dot products, and we cannot manipulate the sigmoid function.
In order to minimize the cost, we need to find the weight and bias values for which the cost function returns the smallest value possible. The smaller the cost, the more correct our predictions are.
To find the minima of a function, we can use the gradient descent algorithm. The gradient descent can be mathematically represented as:


𝛛Error is the cost function. The above equation tells us to find the partial derivative of the cost function with respect to each weight and bias and subtract the result from the existing weights to get new weights.
The derivative of a function gives us its slope at any given point. To find if the cost increases or decreases, given the weight value, we can find the derivative of the function at that particular weight value. If the cost increases with the increase in weight, the derivative will return a positive value which will then be subtracted from the existing value.
On the other hand, if the cost is decreasing with an increase in weight, a negative value will be returned, which will be added to the existing weight value since negative into negative is positive.
In the above equation a is called the learning rate, which is multiplied by the derivative. The learning rate decides how fast our algorithm learns.
We need to repeat the execution of gradient descent for all the weights and biases until the cost is minimized and for which the cost function returns a value close to zero.
Now is the time to implement what we have studied so far. We will create a simple neural network with one input and one output layer in Python.
Comments
Post a Comment