Max-pooling / Pooling in Neural Networks
Max-pooling / Pooling
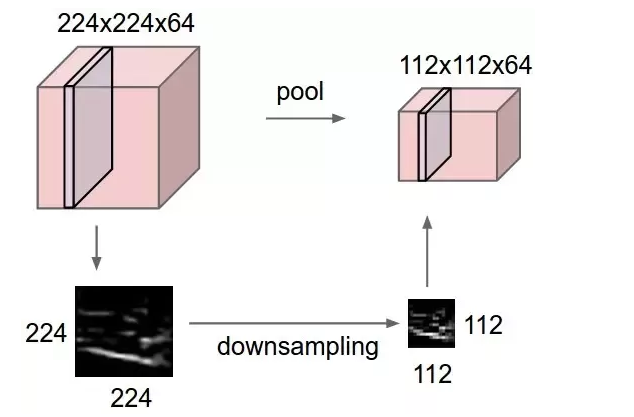
Max pooling is a sample-based discretization process. The objective is to down-sample an input representation (image, hidden-layer output matrix, etc.), reducing its dimensionality and allowing for assumptions to be made about features contained in the sub-regions binned.[2]
How does it work and why[edit]
This is done to in part to help over-fitting by providing an abstracted form of the representation. As well, it reduces the computational cost by reducing the number of parameters to learn and provides basic translation invariance to the internal representation.
Max pooling is done by applying a max filter to (usually) non-overlapping subregions of the initial representation.
Examples[edit]
Let's say we have a 4x4 matrix representing our initial input. Let's say, as well, that we have a 2x2 filter that we'll run over our input. We'll have a stride of 2 (meaning the (dx, dy) for stepping over our input will be (2, 2)) and won't overlap regions.
For each of the regions represented by the filter, we will take the max of that region and create a new, output matrix where each element is the max of a region in the original input.
Pictorial representation: 
Real-life example: 
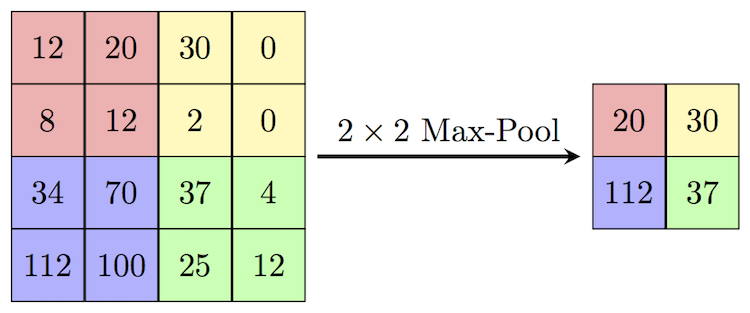
Comments
Post a Comment