Example of Cross-Entropy as a Loss Function

Cross-Entropy as a Loss Function

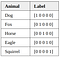
Let’s say we have a dataset of animal images and there are five different animals. Each image has only one animal in it.
Source: 
Each image is labeled with the corresponding animal using the one-hot encoding.
We can treat one hot encoding as a probability distribution for each image. Let’s see a few examples.
The probability distribution of the first image being a dog is 1.0 (=100%).
For the second image, the label tells us that it is a fox with 100% certainty.
…and so on.
As such, the entropy of each image is all zero.
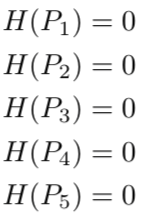
In other words, one-hot encoded labels tell us what animal each image has with 100% certainty. It is not like the first image can be a dog for 90% and a cat for 10%. It is always a dog, and there will be no surprise.
Now, let’s say we have a machine learning model that classifies those images. When we have not adequately trained the model, it may classify the first image (dog) as follows:
The model says the first image is 40% for a dog, 30% for a fox, 5% for a horse, 5% for an eagle and 20% for a squirrel. This estimation is not very precise or confident about what animal the first image has.
In contrast, the label gives us the exact distribution of the first image’s animal class. It tells us it is a dog with 100% certainty.
So, how well was the model’s prediction? We can calculate the cross-entropy as follows:
This is higher than the zero entropy of the label but we do not have an intuitive sense of what this value means. So, let’s see another cross-entropy value for comparison.
After the model is well trained, it may produce the following prediction for the first image.
As below, the cross-entropy is much lower than before.
The cross-entropy compares the model’s prediction with the label which is the true probability distribution. The cross-entropy goes down as the prediction gets more and more accurate. It becomes zero if the prediction is perfect. As such, the cross-entropy can be a loss function to train a classification model.

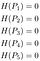
Comments

Post a Comment

Popular posts from this blog

Maxpooling vs minpooling vs average pooling

Image
Pooling is performed in neural networks to reduce variance and computation complexity. Many times, beginners blindly use a pooling method without knowing the reason for using it. Here is a comparison of three basic pooling methods that are widely used. The three types of pooling operations are: Max pooling: The maximum pixel value of the batch is selected. Min pooling: The minimum pixel value of the batch is selected. Average pooling: The average value of all the pixels in the batch is selected. The batch here means a group of pixels of size equal to the filter size which is decided based on the size of the image. In the following example, a filter of 9x9 is chosen. The output of the pooling method varies with the varying value of the filter size. The operations are illustrated through the following figures. Average, Max and Min pooling of size 9x9 applied on an image We cannot say that a particular pooling method is better over others generally. The choice of pooling operation is made...
Read more

Percentiles, Deciles, and Quartiles

Image
Percentiles Percentile: the value below which a percentage of data falls. Example: You are the fourth tallest person in a group of 20 80% of people are shorter than you: That means you are at the  80th percentile . If your height is 1.85m then "1.85m" is the 80th percentile height in that group. In Order Have the data  in order , so you know which values are above and below. To calculate percentiles of height: have the data in height order (sorted by height). To calculate percentiles of age: have the data in age order. And so on. Grouped Data When the data is grouped: Add up all percentages  below  the score, plus  half  the percentage  at  the score. Example: You Score a B! In the test 12% got D, 50% got C, 30% got B and 8% got A You got a B, so add up all the 12% that got D, all the 50% that got C, half of the 30% that got B, for a total percentile of 12% + 50% + 15% =  77% In other words you...
Read more

Data Warehouse Vs Data Mart

Image
What is Data Warehouse? A Data Warehouse collects and manages data from varied sources to provide meaningful business insights. It is a collection of data that is separate from the operational systems and supports the decision making of the company. In Data Warehouse, data is stored from a historical perspective. The data in the warehouse is extracted from multiple functional units. It is checked, cleansed and then integrated with the Data warehouse system. Data warehouse used a very fast computer system having large storage capacity. This tool can answer any complex queries relating to data. What is Data Mart? A data mart is a simple form of a Data Warehouse. It is focused on a single subject. Data Mart draws data from only a few sources. These sources may be central Data warehouse, internal operational systems, or external data sources. A Data Mart is an index and extraction system. It is an important subset of a data warehouse. It is subject-oriented, and it is desig...
Read more