Scale and Normalize Data in Python

Get our environment set up

The first thing we’ll need to do is load in the libraries and datasets we’ll be using.
Now that we’re set up, let’s learn about scaling & normalization. (If you like, you can take this opportunity to take a look at some of the data.)

Scaling vs. Normalization: What’s the difference?

One of the reasons that it’s easy to get confused between scaling and normalization is because the terms are sometimes used interchangeably and, to make it even more confusing, they are very similar! In both cases, you’re transforming the values of numeric variables so that the transformed data points have specific helpful properties. The difference is that, in scaling, you’re changing the range of your data while in normalization you’re changing the shape of the distribution of your data. Let’s talk a little more in-depth about each of these options.

Scaling

This means that you’re transforming your data so that it fits within a specific scale, like 0–100 or 0–1. You want to scale data when you’re using methods based on measures of how far apart data points, like support vector machines, or SVM or k-nearest neighbors, or KNN. With these algorithms, a change of “1” in any numeric feature is given the same importance.
For example, you might be looking at the prices of some products in both Yen and US Dollars. One US Dollar is worth about 100 Yen, but if you don’t scale your prices methods like SVM or KNN will consider a difference in price of 1 Yen as important as a difference of 1 US Dollar! This clearly doesn’t fit with our intuitions of the world. With currency, you can convert between currencies. But what about if you’re looking at something like height and weight? It’s not entirely clear how many pounds should equal one inch (or how many kilograms should equal one meter).
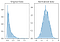
By scaling your variables, you can help compare different variables on equal footing. To help solidify what scaling looks like, let’s look at a made-up example. (Don’t worry, we’ll work with real data in just a second, this is just to help illustrate my point.)
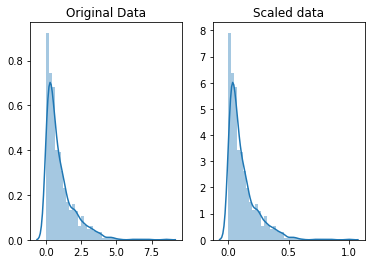
Notice that the shape of the data doesn’t change, but that instead of ranging from 0 to 8ish, it now ranges from 0 to 1.

Normalization

Scaling just changes the range of your data. Normalization is a more radical transformation. The point of normalization is to change your observations so that they can be described as a normal distribution.
Normal distribution: Also known as the “bell curve”, this is a specific statistical distribution where a roughly equal observations fall above and below the mean, the mean and the median are the same, and there are more observations closer to the mean. The normal distribution is also known as the Gaussian distribution.
In general, you’ll only want to normalize your data if you’re going to be using a machine learning or statistics technique that assumes your data is normally distributed. Some examples of these include t-tests, ANOVAs, linear regression, linear discriminant analysis (LDA) and Gaussian naive Bayes. (Pro tip: any method with “Gaussian” in the name probably assumes normality.)
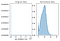
The method we were using to normalize here is called the Box-Cox Transformation. Let’s take a quick peek at what normalizing some data looks like:
Notice that the shape of our data has changed. Before normalizing it was almost L-shaped. But after normalizing it looks more like the outline of a bell (hence “bell curve”).

Your turn!

For the following example, decide whether scaling or normalization makes more sense.
  • You want to build a linear regression model to predict someone’s grades given how much time they spend on various activities during a normal school week. You notice that your measurements for how much time students spend studying aren’t normally distributed: some students spend almost no time studying and others study for four or more hours every day. Should you scale or normalize this variable?
  • You’re still working on your grades study, but you want to include information on how students perform on several fitness tests as well. You have information on how many jumping jacks and push-ups each student can complete in a minute. However, you notice that students perform far more jumping jacks than push-ups: the average for the former is 40 and for the latter only 10. Should you scale or normalize these variables?

Practice scaling

To practice scaling and normalization, we’re going to be using a dataset of Kickstarter campaigns. (Kickstarter is a website where people can ask people to invest in various projects and concept products.)
Let’s start by scaling the goals of each campaign, which is how much money they were asking for.

Practice normalization

Ok, now let’s try practicing normalization. We’re going to normalize the amount of money pledged to each campaign.

Comments

Post a Comment

Popular posts from this blog

Maxpooling vs minpooling vs average pooling

Image
Pooling is performed in neural networks to reduce variance and computation complexity. Many times, beginners blindly use a pooling method without knowing the reason for using it. Here is a comparison of three basic pooling methods that are widely used. The three types of pooling operations are: Max pooling: The maximum pixel value of the batch is selected. Min pooling: The minimum pixel value of the batch is selected. Average pooling: The average value of all the pixels in the batch is selected. The batch here means a group of pixels of size equal to the filter size which is decided based on the size of the image. In the following example, a filter of 9x9 is chosen. The output of the pooling method varies with the varying value of the filter size. The operations are illustrated through the following figures. Average, Max and Min pooling of size 9x9 applied on an image We cannot say that a particular pooling method is better over others generally. The choice of pooling operation is made...
Read more

Generative AI - Prompting with purpose: The RACE framework for data analysis

Image
  Prompting with purpose: The RACE framework for data analysis We've already established that the quality of your prompts directly influences the quality of your AI-generated outputs. A well-crafted prompt acts as a guiding light, leading the AI toward insightful and actionable results. But how can we consistently achieve this level of clarity and precision in our prompts? Let’s look into the RACE framework—an invaluable tool to elevate your prompts, ensuring they are clear, insightful, and evidence-based. This framework offers a structured approach to prompt engineering, helping you break down complex tasks into manageable steps and communicate your intentions effectively to the AI. This reading will assist you with developing a powerful methodology with generative AI for your data analysis tasks, leading to more accurate, relevant, and impactful results. What is the RACE framework? RACE is an acronym that stands for Research, Answer, Cite, and Expand. It serves as a valuable fram...
Read more

Best Practices for Storing and Loading JSON Objects from a Large SQL Server Table Using .NET Core

 Best Practices for Storing and Loading JSON Objects from a Large SQL Server Table Using .NET Core Introduction JSON (JavaScript Object Notation) is widely used for storing structured data in SQL Server. However, when dealing with large tables, inefficient handling of JSON data can lead to performance bottlenecks, high storage costs, and slow queries. In this article, we will cover best practices for saving and loading JSON objects from large SQL Server tables using .NET Core. We will focus on storage strategies, indexing, efficient querying, and optimized data retrieval using Entity Framework Core (EF Core) and Dapper. --- 1. Choosing the Right Storage Strategy SQL Server supports JSON natively, but choosing the correct storage method depends on your use case. Option 1: Store JSON as NVARCHAR(MAX) (Best for Flexibility & Simplicity) ✔ Ideal for semi-structured or frequently changing data. ✔ Suitable when you need to store the entire JSON object but rarely query individual fiel...
Read more