Correlation

Correlation

When the two sets of data are strongly linked together we say they have a High Correlation.
The word Correlation is made of Co- (meaning "together"), and Relation
  • Correlation is Positive when the values increase together, and
  • Correlation is Negative when one value decreases as the other increases
Like this:
correlation levels
(Learn More About Correlation)

Negative Correlation

Correlations can be negative, which means there is a correlation but one value goes down as the other value increases.

Example : Birth Rate vs Income

The birth rate tends to be lower in richer countries.

Below is a scatter plot for about 100 different countries.
CountryYearly
Production
per Person		Birth
Rate
Madagascar$8005.70
India$3,1002.85
Mexico$9,6002.49
Taiwan$25,3001.57
Norway$40,0001.78
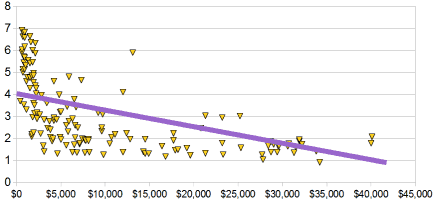
gdp vs birth rate
It has a negative correlation (the line slopes down)
Note: I tried to fit a straight line to the data, but maybe a curve would work better, what do you think?


How To Calculate

How did I calculate the value 0.9575 at the top?
I used "Pearson's Correlation". There is software that can calculate it, such as the CORREL() function in Excel or LibreOffice Calc ...

... but here is how to calculate it yourself:

Let us call the two sets of data "x" and "y" (in our case Temperature is x and Ice Cream Sales is y):
  • Step 1: Find the mean of x, and the mean of y
  • Step 2: Subtract the mean of x from every x value (call them "a"), do the same for y (call them "b")
  • Step 3: Calculate: ab, a2 and b2 for every value
  • Step 4: Sum up ab, sum up a2 and sum up b2
  • Step 5: Divide the sum of ab by the square root of [(sum of a2) × (sum of b2)]
Here is how I calculated the first Ice Cream example (values rounded to 1 or 0 decimal places):
correlation calculations
As a formula it is:
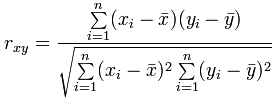
correlation formula
Where:
  • Σ is Sigma, the symbol for "sum up"
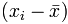  • correlation formula (xi - xbar) is each x-value minus the mean of x (called "a" above)
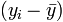  • correlation formula (yi - ybar) is each y-value minus the mean of y (called "b" above)
You probably won't have to calculate it like that, but at least you know it is not "magic", but simply a routine set of calculations.

Note for Programmers

You can calculate it in one pass through the data. Just sum up x, y, x2, y2 and xy (no need for a or b calculations above) then use the formula:
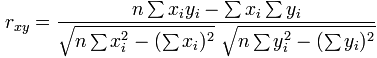
correlation formula onepass

Other Methods

There are other ways to calculate a correlation coefficient, such as "Spearman's rank correlation coefficient".

Comments

Post a Comment

Popular posts from this blog

Maxpooling vs minpooling vs average pooling

Image
Pooling is performed in neural networks to reduce variance and computation complexity. Many times, beginners blindly use a pooling method without knowing the reason for using it. Here is a comparison of three basic pooling methods that are widely used. The three types of pooling operations are: Max pooling: The maximum pixel value of the batch is selected. Min pooling: The minimum pixel value of the batch is selected. Average pooling: The average value of all the pixels in the batch is selected. The batch here means a group of pixels of size equal to the filter size which is decided based on the size of the image. In the following example, a filter of 9x9 is chosen. The output of the pooling method varies with the varying value of the filter size. The operations are illustrated through the following figures. Average, Max and Min pooling of size 9x9 applied on an image We cannot say that a particular pooling method is better over others generally. The choice of pooling operation is made...
Read more

Generative AI - Prompting with purpose: The RACE framework for data analysis

Image
  Prompting with purpose: The RACE framework for data analysis We've already established that the quality of your prompts directly influences the quality of your AI-generated outputs. A well-crafted prompt acts as a guiding light, leading the AI toward insightful and actionable results. But how can we consistently achieve this level of clarity and precision in our prompts? Let’s look into the RACE framework—an invaluable tool to elevate your prompts, ensuring they are clear, insightful, and evidence-based. This framework offers a structured approach to prompt engineering, helping you break down complex tasks into manageable steps and communicate your intentions effectively to the AI. This reading will assist you with developing a powerful methodology with generative AI for your data analysis tasks, leading to more accurate, relevant, and impactful results. What is the RACE framework? RACE is an acronym that stands for Research, Answer, Cite, and Expand. It serves as a valuable fram...
Read more

Best Practices for Storing and Loading JSON Objects from a Large SQL Server Table Using .NET Core

 Best Practices for Storing and Loading JSON Objects from a Large SQL Server Table Using .NET Core Introduction JSON (JavaScript Object Notation) is widely used for storing structured data in SQL Server. However, when dealing with large tables, inefficient handling of JSON data can lead to performance bottlenecks, high storage costs, and slow queries. In this article, we will cover best practices for saving and loading JSON objects from large SQL Server tables using .NET Core. We will focus on storage strategies, indexing, efficient querying, and optimized data retrieval using Entity Framework Core (EF Core) and Dapper. --- 1. Choosing the Right Storage Strategy SQL Server supports JSON natively, but choosing the correct storage method depends on your use case. Option 1: Store JSON as NVARCHAR(MAX) (Best for Flexibility & Simplicity) ✔ Ideal for semi-structured or frequently changing data. ✔ Suitable when you need to store the entire JSON object but rarely query individual fiel...
Read more