What Does Derivatives Mean in Real World

Introduction to Derivatives

It is all about slope!

Slope = Change in YChange in X

We can find an average slope between two points.
But how do we find the slope at a point? There is nothing to measure!
But with derivatives we use a small difference ... ... then have it shrink towards zero.

Let us Find a Derivative!

To find the derivative of a function y = f(x) we use the slope formula:

Slope = Change in YChange in X = ΔyΔx

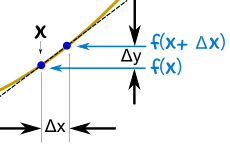
And (from the diagram) we see that:

x changes from		x	to	x+Δx
y changes from		f(x)	to	f(x+Δx)

Now follow these steps:

• Fill in this slope formula: ΔyΔx = f(x+Δx) − f(x)Δx
• Simplify it as best we can
• Then make Δx shrink towards zero.

Like this:

Example: the function f(x) = x²

We know f(x) = x², and we can calculate f(x+Δx) :

Start with:		f(x+Δx) = (x+Δx)2
Expand (x + Δx)2:		f(x+Δx) = x2 + 2x Δx + (Δx)2

The slope formula is:f(x+Δx) − f(x)Δx

Put in f(x+Δx) and f(x):x² + 2x Δx + (Δx)² − x²Δx

Simplify (x² and −x² cancel):2x Δx + (Δx)²Δx

Simplify more (divide through by Δx):= 2x + Δx

Then as Δx heads towards 0 we get:= 2x

Result: the derivative of x² is 2x

In other words, the slope at x is 2x

We write dx instead of "Δx heads towards 0".

And "the derivative of" is commonly written  :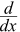

x² = 2x
"The derivative of x² equals 2x"
or simply "d dx of x² equals 2x"

What does 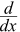x² = 2x mean?

It means that, for the function x², the slope or "rate of change" at any point is 2x.

So when x=2 the slope is 2x = 4, as shown here:

Or when x=5 the slope is 2x = 10, and so on.

Note: sometimes f’(x) is also used for "the derivative of":

f’(x) = 2x
"The derivative of f(x) equals 2x"
or simply "f-dash of x equals 2x"

Let's try another example.

Example: What is x³ ?

We know f(x) = x³, and can calculate f(x+Δx) :

Start with:		f(x+Δx) = (x+Δx)3
Expand (x + Δx)3:		f(x+Δx) = x3 + 3x2 Δx + 3x (Δx)2 + (Δx)3

The slope formula:f(x+Δx) − f(x)Δx

Put in f(x+Δx) and f(x):x³ + 3x² Δx + 3x (Δx)² + (Δx)³ − x³Δx

Simplify (x³ and −x³ cancel):3x² Δx + 3x (Δx)² + (Δx)³Δx

Simplify more (divide through by Δx):= 3x² + 3x Δx + (Δx)²

Then as Δx heads towards 0 we get:= 3x²

Result: the derivative of x³ is 3x²

Have a play with it using the Derivative Plotter.

Derivatives of Other Functions

We can use the same method to work out derivatives of other functions (like sine, cosine, logarithms, etc).

But in practice the usual way to find derivatives is to use:

Derivative Rules

Example: what is the derivative of sin(x) ?

On Derivative Rules it is listed as being cos(x)
Done.

Using the rules can be tricky!

Example: what is the derivative of cos(x)sin(x) ?

You can't just find the derivative of cos(x) and multiply it by the derivative of sin(x) ... you must use the "Product Rule" as explained on the Derivative Rules page.
It actually works out to be cos²(x) − sin²(x)

So that is your next step: learn how to use the rules.

Notation

"Shrink towards zero" is actually written as a limit like this:

"The derivative of f equals the limit as Δx goes to zero of f(x+Δx) - f(x) over Δx"

Or sometimes the derivative is written like this (explained on Derivatives as dy/dx):

 

The process of finding a derivative is called "differentiation".

You do differentiation ... to get a derivative.

Where