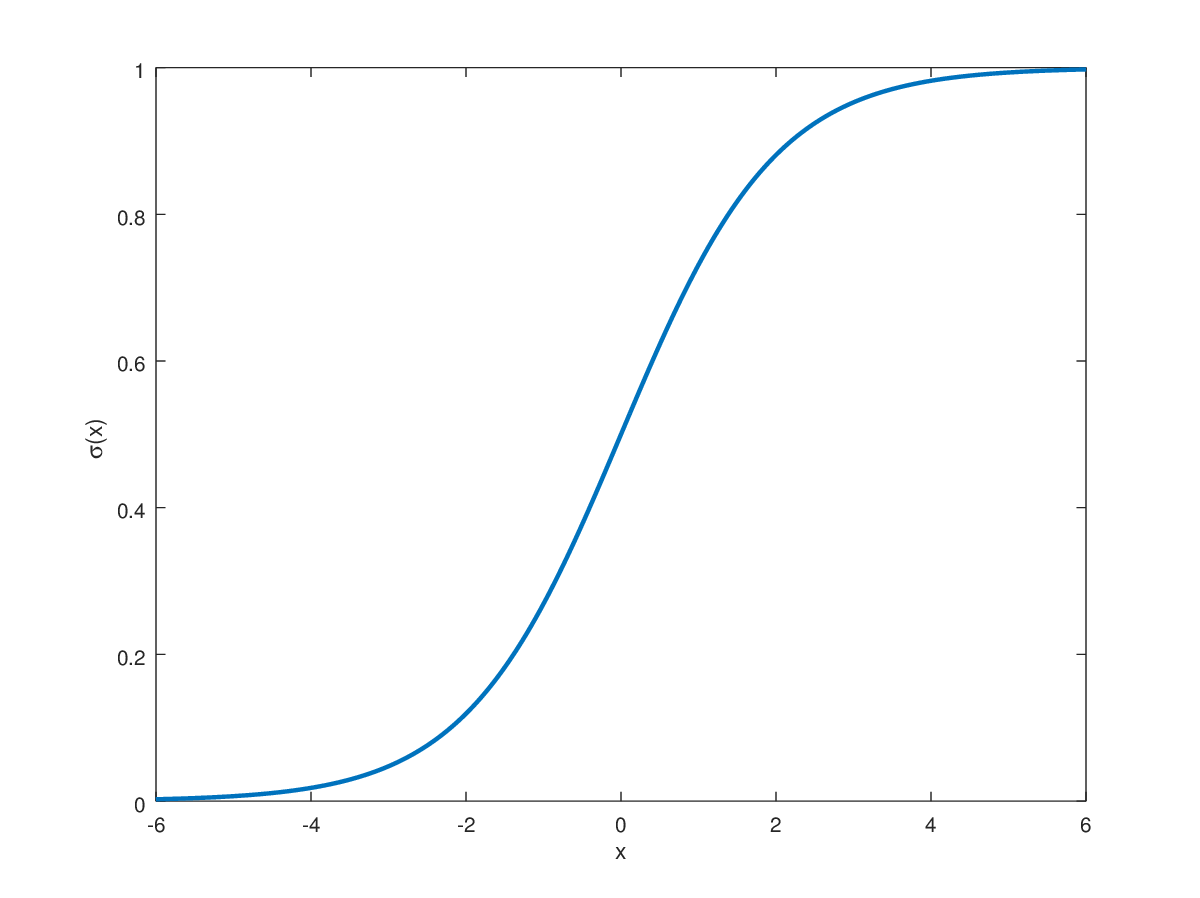
The Sigmoid Function (the logistic function)

The sigmoid function is a continuous, monotonically increasing function with a characteristic 'S'-like curve, and possesses several interesting properties that make it an obvious choice as an activation function for nodes in artificial neural networks.
The domain of the sigmoid function is the set of all real numbers, R, and it's defined as:

Please note that equation (1) could just as well be written as σ(x)=exex+1 (this is seen by multiplying equation (1) by exex, i.e. multiplying by 1).(1)σ(x)=11+e−x
The graph of the sigmoid function illustrates its smooth, gradual transition from values just above 0 to values just below 1 - a transition that almost fully occurs in the interval −5<x<5.
For arguments near 0 the sigmoid function approximates a linear function with slope 14.
The elongated 'S'-like curve of the sigmoid function Figure 1: The elongated 'S'-like curve of the sigmoid function

Decision Boundary:
Means the value at which we split our suggested labels to either 0s or 1s.

Comments

Post a Comment

Popular posts from this blog

Maxpooling vs minpooling vs average pooling

Image
Pooling is performed in neural networks to reduce variance and computation complexity. Many times, beginners blindly use a pooling method without knowing the reason for using it. Here is a comparison of three basic pooling methods that are widely used. The three types of pooling operations are: Max pooling: The maximum pixel value of the batch is selected. Min pooling: The minimum pixel value of the batch is selected. Average pooling: The average value of all the pixels in the batch is selected. The batch here means a group of pixels of size equal to the filter size which is decided based on the size of the image. In the following example, a filter of 9x9 is chosen. The output of the pooling method varies with the varying value of the filter size. The operations are illustrated through the following figures. Average, Max and Min pooling of size 9x9 applied on an image We cannot say that a particular pooling method is better over others generally. The choice of pooling operation is made...
Read more

Generative AI - Prompting with purpose: The RACE framework for data analysis

Image
  Prompting with purpose: The RACE framework for data analysis We've already established that the quality of your prompts directly influences the quality of your AI-generated outputs. A well-crafted prompt acts as a guiding light, leading the AI toward insightful and actionable results. But how can we consistently achieve this level of clarity and precision in our prompts? Let’s look into the RACE framework—an invaluable tool to elevate your prompts, ensuring they are clear, insightful, and evidence-based. This framework offers a structured approach to prompt engineering, helping you break down complex tasks into manageable steps and communicate your intentions effectively to the AI. This reading will assist you with developing a powerful methodology with generative AI for your data analysis tasks, leading to more accurate, relevant, and impactful results. What is the RACE framework? RACE is an acronym that stands for Research, Answer, Cite, and Expand. It serves as a valuable fram...
Read more

Best Practices for Storing and Loading JSON Objects from a Large SQL Server Table Using .NET Core

 Best Practices for Storing and Loading JSON Objects from a Large SQL Server Table Using .NET Core Introduction JSON (JavaScript Object Notation) is widely used for storing structured data in SQL Server. However, when dealing with large tables, inefficient handling of JSON data can lead to performance bottlenecks, high storage costs, and slow queries. In this article, we will cover best practices for saving and loading JSON objects from large SQL Server tables using .NET Core. We will focus on storage strategies, indexing, efficient querying, and optimized data retrieval using Entity Framework Core (EF Core) and Dapper. --- 1. Choosing the Right Storage Strategy SQL Server supports JSON natively, but choosing the correct storage method depends on your use case. Option 1: Store JSON as NVARCHAR(MAX) (Best for Flexibility & Simplicity) ✔ Ideal for semi-structured or frequently changing data. ✔ Suitable when you need to store the entire JSON object but rarely query individual fiel...
Read more